TRIZ理论属于工程哲学，既然是哲学，就得飘逸点儿，因为哲学与其他学科往往同理。该理论属于研究生和博士阶段的内容，但既然是哲学，对于各个阶段的学习也是有指导意义的。今天讲讲利用TRIZ中突破思维惯性的方法来帮助孩子们学好数学。 在经典TRIZ理论中有五种突破思维惯性的方法，今天重点讲讲STC算子法。 什么是STC算子？ 技术系统都有尺寸、时间和成本等因素，通过把这些因素推到无穷大和无穷小，激化某些矛盾，从而突破思维的惯性或获得特殊的结论。其实，在实际应用中，完全没有必要受上述参数的约束，本着上述思想，可以扩大到任何的参数。哲学的问题就是不能照本宣科，墨守成规。接下来我们来以一道小学四年级的数学题为例，看看这种极限思维的方法，如何应用到解题上。

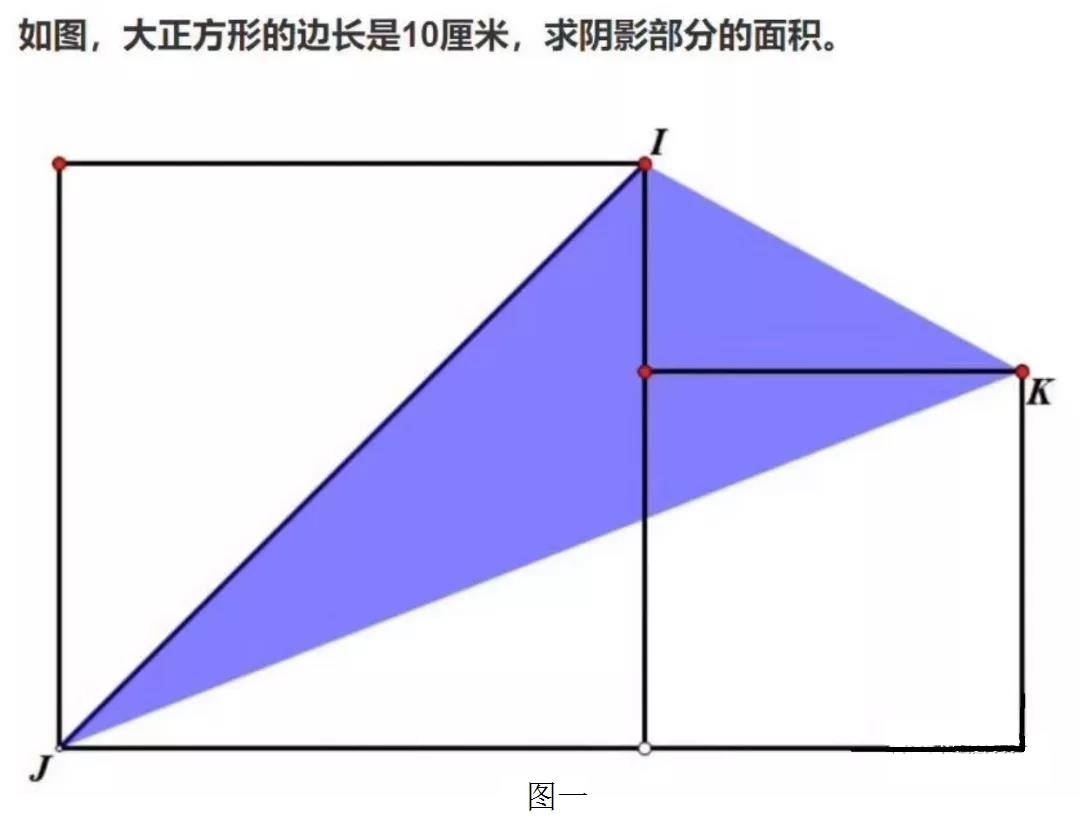
请在这里停留五分钟，看看大家能否口算这道题的答案呢？

这道题，只提供了大正方形的边长，而没有限制小正方形的边长。换句话说小正方形的边长是可变的，同时，阴影部分的形状也是在不断变化的，但是因为某种约束，面积是恒定的。既然面积是恒定的，那么我们只要算出各种变化中的一个面积，即可以把题解出。在这种情况下，我们就可以把参数推向两端，从而激化矛盾。

第一种情况，把右侧的小正方形推向无穷小，是不是可以呢？那图形就变成了图二的形状。因为小正方形无穷小，所以K点就到了大正方形的右下角。这个时候，阴影面积正好无限接近半个大正方形。大正方形的面积是10（cm）*10（cm）=100（cm²），那么一半就是50cm²。

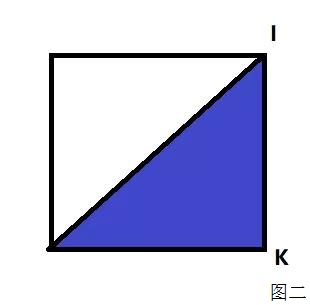
除了上述方法，还可以向另外一端推动参数，即把小正方形放大。虽然小正方形放大，但不能放到无穷大，关键是要找到一个特殊位置，便于计算。小正方形和大正方形同样大的时候，又会出现一个特殊位置，如图三。

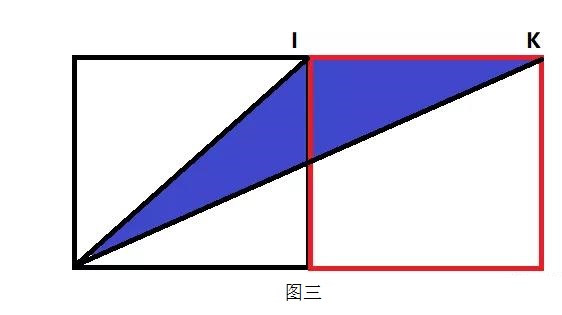
这个时候三角形的面积也是可以口算的。底是10cm，高是10cm，三角形的面积是50cm²，和上边计算的结果是相同，对之前的结果进行了佐证。这道题就是利用极限思维，进行求解的一个非常好的例子。

这种利用参数的不断变化，在数学公式的理解中也有很多应用。利用好了这个方法，可以事半功倍的学好数学。

下面我们再来看看梯形、正方形、平行四边形、长方形和三角形的公式有什么内在联系？让我们先看看梯形的面积公式，如图四：S=（a+b）*h/2，即：（上底+下底）*高/2。大家都知道，不赘述。

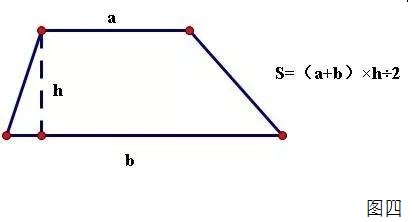
与平行四边形的关系：

平行四边形可以看成特殊的梯形，所以，上底=下底=平行四边形的底，高=高。带入梯形的公式就是：

S=（平行四边形的底+平行四边形的底）*高/2

所以，长方形的公式就变化为：S=平行四边形的底*高；

 

与长方形什么关系呢：

长方形可以看成特殊的梯形，所以，上底=下底=长，宽=高。带入梯形的公式就是：

S=（长+长）*宽/2

所以，长方形的公式就变化为：S=长*宽；

 

与正方形的关系：

正方形也可以看成特殊的梯形，所以，上底=下底=高=边长。带入梯形的公式就是：

S=（边长+边长）*边长/2

所以，正方形的公式就变化为：S=边长*边长；

 

与三角形的关系:

三角形就是上底为0的梯形，所以，上底=0，下底=底，高=高。带入梯形的公式就是：

S=（0+底）*高/2

所以，三角形的公式就变为：S=底*高/2；

   总结起来，这些公式都是一个！其实在整个中学和大学阶段，这种情况会反复出现。

如图五，这是相对论质量的公式。从这个公式可以看出，在宏观低速时，因为速度相对于光速是趋近于零的，因此分母趋近于1，运动物体的质量近似为静止质量。因此，牛顿第二定律是不精确的，实际是个宏观低速近似值。

    在大学的普通物理里磁场相关的计算中，也有大量的公式，其实也是参数在不同特殊情况下的变换。

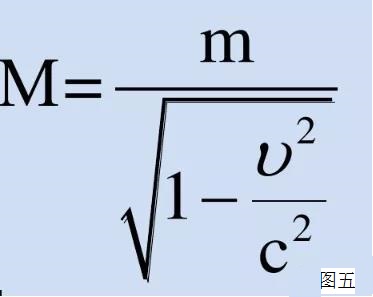
综上所述，其实在学习过程中，找到知识与知识的联系，融会贯通才是学好知识、用好知识的关键。解决技术问题亦是如此！